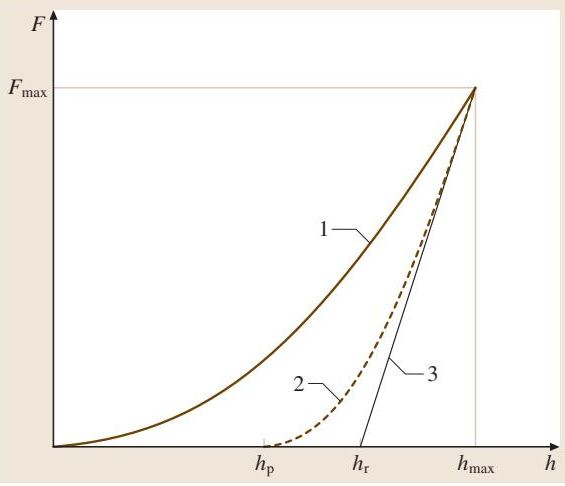
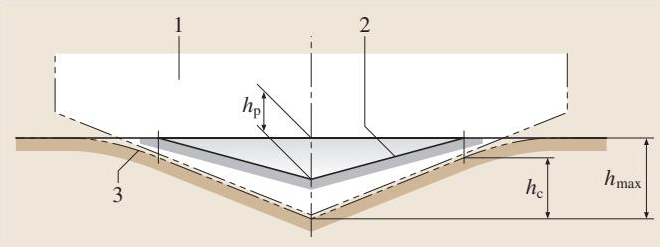
仪器化压痕试验(Instrumented Indentation Test, IIT),常被业界称为纳米压痕技术,它标志着材料硬度测试从单一数值向多维度力学性能表征的飞跃。传统硬度测试依赖于光学显微镜测量压痕尺寸,而IIT通过连续监测压入力与压入深度的完整过程,不仅能得到与传统方法等效的硬度值,更重要的是,它能够揭示材料的压入模量、弹塑性硬度等一系列深层次的力学性能参数。这一切,都无需对压痕进行光学成像。 该技术的核心在于,使用一个比被测材料硬得多的压头,以精确控制的力或位移加载到样品表面。整个加载-卸载循环中的力和深度数据被实时记录下来,形成一条标志性的力-深度曲线(见图1)。 根据测试需求,可以选择不同几何形状的压头: 1. 维氏压头 (Vickers pyramid):标准的四方底正交角锥体金刚石压头,对顶面夹角 α = 136°。 2. 伯克维奇压头 (Berkovich pyramid):三棱锥金刚石压头,因其尖端更容易加工到原子级锋利,在纳米尺度测试中应用极广。 3. 硬质合金球 (Hardmetal ball):特别适用于测定材料的弹性行为。 4. 球形金刚石压头 (Diamond spherical indenter)。 测试过程可以是力控制或位移控制。在测量时间相关效应(如蠕变或应力松弛)时: • 力控制法:在指定时间内保持测试力恒定,测量压入深度随保载时间的变化。 • 位移控制法:在指定时间内保持压入深度恒定,测量测试力随保载时间的变化。 • 微观尺度效应:当压入深度小于1 μm时,压头尖端的真实几何形状对机械变形行为有显著影响。因此,为了保证不同设备间测试结果的可重复性,对仪器和压头形状的精确标定是必不可少的。 • 压头损伤与变形:在高接触压力下,压头可能受损。因此,在大于2N的力程范围内,常使用硬质合金压头。当测试具有极高硬度和弹性模量的样品时,必须考虑压头自身变形对测试结果的影响。 • 零点确定:为了准确测定力和对应的压入深度,每次测试都必须独立确定力/深度测量的零点。 下表列出了仪器化压痕试验中常用的符号和名称。 表1 仪器化压痕试验的符号与名称 表2 仪器化压痕试验的参数及对测试结果有影响的附加因素 马氏硬度是在施加测试力的情况下测量的,它包含了材料的塑性变形和弹性变形,因此这个硬度值可以为所有类型的材料计算。它通常根据加载力/深度曲线在达到指定测试力时的数值确定。 马氏硬度定义为测试力 F 除以压头侵入接触零点以下的表面积 As(h),单位为 N/mm²。 • 维氏压头: • 伯克维奇压头: 马氏硬度的命名方式包含了测试条件。例如: • HM: 马氏硬度符号 • 0.5: 测试力 (N) • 20: 测试力施加时间 (s) • 20: 测试力保载时间 (s) • 8700 N/mm²: 硬度值 压入硬度 HIT 是衡量材料抵抗永久变形或损伤能力的指标,这一定义与Meyer首次提出的普遍接受的硬度定义一致。 • 对于压入深度 < 6 μm:压头尖端不可避免地存在一定程度的钝化,球形压头的半径也并非完全均匀。此时,不能假设压头的面积函数是其理论形状,必须精确测定给定压头的实际面积函数。 • 对于压入深度 > 6 μm:可采用理论形状作为投影面积 Ap 的初步近似。 • 理想维氏压头: • 理想伯克维奇压头: • 修正伯克维奇压头: 这里的接触深度 hc 是关键,它通过以下公式计算,以校正表面弹性位移的影响: 表3 不同压头几何形状的校正因子 ε 压入模量 EIT 与材料的杨氏模量相当,可以从计算压入硬度 HIT 的卸载曲线切线斜率中计算得出。 • νs: 试样的泊松比 • νi: 压头的泊松比 (金刚石为 0.07) • Er: 压痕接触的折合模量 • Ei: 压头的模量 (金刚石为 1.14 × 106 N/mm²) • Cs: 接触柔度,即在最大测试力处评估的(已进行机架刚度校正的)测试力移除曲线的 dh/dF • β: 不同尖端几何形状的校正因子 (见表4) 表4 不同压头几何形状的校正因子 β 涂层的弹塑性是决定涂层产品性能的关键。许多涂层,特别是耐磨涂层,其核心价值就体现在高硬度上。因此,测量涂层硬度是质量控制的重要工具,而杨氏模量则在涂层部件的设计和应力计算中至关重要。 使用仪器化压痕法测定块体材料的硬度和模量相对直接,但当测量对象是涂层时,问题变得复杂。测试结果会受到涂层厚度和基底性能的共同影响。那么,在实际测试中,我们如何剥离基底对涂层性能测量的影响呢? 1. 桩-积效应 (Pile-up) 2. 仪器检定与校准 3. 压头选择 • 测塑性 (硬度):推荐使用尖锐压头(如维氏、伯克维奇),涂层越薄,压头应越尖锐。 • 测弹性 (模量):推荐使用球形压头,理想情况是使用大半径球头,以便在合理的压入位移范围内实现纯弹性压痕。 4. 试样制备与状态 • 表面平整度与粗糙度:样品表面应尽可能光滑。一般建议,表面粗糙度 Ra 值应小于最大压入深度的5%。粗糙的表面会增加结果的离散性。对于伯克维奇压头,当局部表面法线与压痕轴的夹角大于7°时,才会产生显著误差。 • 机械抛光:抛光可能会改变表面的加工硬化状态或残余应力,从而影响测量硬度。对于金属而言尤其如此。抛光也会减薄涂层,增强基底效应,因此需要重新测量涂层厚度。应遵循“最少制备”原则。 • 残余应力:涂层中普遍存在残余应力(如热失配应力、沉积应力),因此通常不会有无应力表面。 • 清洁:应避免不必要的清洁程序。如需清洁,应采用最小化损伤的方法,如干燥无油气流吹扫、CO2 升华颗粒流清洗或使用对样品化学惰性的溶剂冲洗。 要精确表征涂层力学性能,从样品制备到参数设置的每一步都充满挑战。这正是专业检测实验室的核心价值所在,能够确保从源头控制变量,提供可靠的科研与品控数据。 精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测涂层纳米压痕硬度与模量,可靠准确。欢迎沟通交流,电话19939716636 5. 测试条件 • 压痕间距:为避免相互影响,压痕应距离界面或自由表面至少为其压痕直径的三倍。对于多点测试,压痕间的最小距离应至少为最大压痕直径的五倍(对于陶瓷和铁基金属)或十倍(对于其他材料)。 • 时间依赖性:材料的蠕变行为对硬度和模量结果有显著影响。对于低硬度/模量比的材料(多数金属),如果保载时间太短,模量结果可能不可靠,误差甚至可能超过50%。建议通过预实验评估蠕变速率,并设置足够的保载时间。 计算出的硬度和模量是涂层/基底组合的“复合性能”。核心任务是从这些复合性能中提取出涂层的本征属性。 1. 剥离基底效应 • 对于软/韧性涂层:选择测试参数,使数据落在 a/tc < 1.5 的区域。通过在一系列不同压深下进行测量,并将压入弹性模量与 a/tc 进行线性拟合,外推至 a/tc = 0 处,即可得到涂层的压入模量 EIT(见图4)。 • 对于硬质涂层/软基底:选择测试参数,使 hc/tc 处于 HIT 达到最大值的范围(通常为 0 < hc/tc < 0.5)。如果在此范围内观察到一个恒定的 HIT 最大值(平台区),这便是涂层的压入硬度。如果仅出现一个峰值,则这只是涂层压入硬度的最小估计值。 2. 测量流程与热漂移校正 精确的测量离不开对仪器本身的深刻理解。仪器的柔度和压头的真实几何形状是两个必须精确标定的核心参数。 基本原理 迭代标定流程 1. 初步估计:在标准参考物质(如熔融石英或钨)上进行一系列不同载荷的压痕测试。使用理想压头几何形状(如 A(hc) = 24.5hc²)作为接触面积的初始估计。 2. 计算 Cf 和 Er:绘制 CT 对 A-1/2 的图,通过线性拟合得到 Cf 和 Er 的初始值。 3. 修正面积函数:使用上一步得到的 Cf 和 Er,反向计算所有压痕的接触面积 AP。然后,用一个多项式函数拟合这些 AP 与 hc 的数据,得到一个更真实的压头面积函数。这个函数不仅包含理想项,还包含了描述尖端钝化的修正项。 4. 迭代:由于精确的面积函数会反过来影响 Cf 和 Er 的计算,因此需要使用新的面积函数重复上述步骤,进行多次迭代,直到所有参数收敛为止。 通过这一严谨的流程,才能确保从原始的力-深度曲线中提取出的硬度、模量等数据真实反映材料的本征力学性能。仪器化压痕试验(IIT)技术深度解析
核心测试原理
测试中的关键考量
符号 名称 单位a,b α 角锥压头的特定角度 度 r 球形压头半径 mm F 测试力 N Fmax 最大测试力 N h 施加测试力下的压入深度 mm hmax Fmax 时的最大压入深度 mm hT Fmax 处卸载曲线切线与深度轴的交点 (见图1) mm hP 卸除测试力后的永久压入深度 mm hC Fmax 时压头与试样的接触深度 mm As(h) 压头在距尖端h处的表面积 mm² Ap(hc) 压头在距尖端hC处的投影接触面积 mm² HM 马氏硬度 N/mm² HMs 由加载力/深度曲线斜率确定的马氏硬度 N/mm² HIT 压入硬度 N/mm² EIT 压入模量 N/mm² CIT 压入蠕变 % RIT 压入松弛 % Wtotal 总压入机械功 Nm Welast 弹性反向变形功 Nm ηIT Welast / Wtotal 的比率 % a 为避免数字过长,可使用单位的倍数或分数。b 1 N/mm² = 1 MPa。 马氏硬度 HM 由斜率确定的马氏硬度 HMs 压入硬度 HIT 压入模量 EIT 压入蠕变 CIT 压入松弛 RIT 压入功 ηIT 施加的测试力 × × × × × × 施加的压入深度 × □ 测试力持续时间 × × × × × × 测试力施加时间 × 恒定测试力下的保持时间 × × × □ 恒定压入深度下的保持时间 × □ 曲线拟合范围内卸除测试力时间 × × □ 压头材料和形状 □ □ □ □ □ □ □ 控制模式(力或深度) □ □ □ □ □ □ □ 压头接近速度 □ □ □ 测试力施加速度 □ □ □ □ 压入深度施加速度 □ □ □ □ 额外保持周期的位置和持续时间 □ □ □ □ 温度 □ □ □ □ □ □ □ × 在测试结果中表述 □ 影响测试结果的附加因素 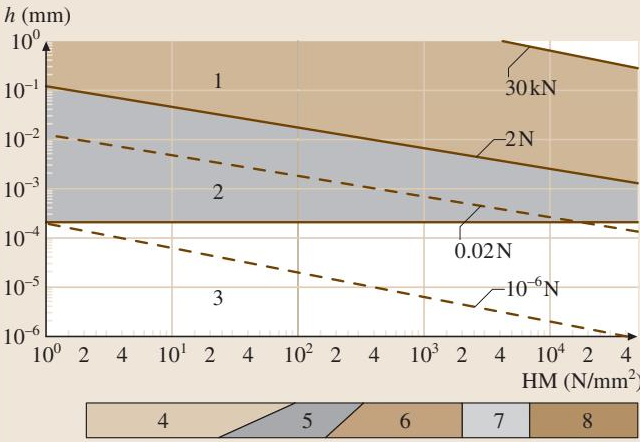
图3 马氏硬度、压入深度和测试力之间的关系(关键点:1-宏观范围;2-微观范围;3-纳米范围;4-橡胶;5-塑料;6-有色金属;7-钢;8-硬质合金、陶瓷)核心力学参数的测定
马氏硬度 (Martens Hardness, HM)
对于理想的维氏和伯克维奇压头,其计算公式分别为:HM 0.5 / 20 / 20 = 8700 N/mm² 表示:压入硬度 (Indentation Hardness, HIT)
其中,Fmax 是最大施加力,Ap 是压头与试样之间的投影接触面积。Ap 是根据力-位移曲线和已知的压头面积函数计算得出的。
其中,hmax 是最大位移,hr 是卸载曲线在 Fmax 点的切线与位移轴的截距,ε 是一个取决于压头几何形状的校正因子(见表3)。压头几何形状 ε 平冲头 1 圆锥 2(π-2)/π = 0.73 旋转抛物面 (包括球形) 3/4 伯克维奇, 维氏 3/4 压入模量 (Indentation Modulus, EIT)
其中:压头几何形状 β 轴对称 (如圆锥, 球形) 1 伯克维奇 1.034 维氏 1.012 纳米压痕方法在涂层表征中的应用
关键挑战与应对策略
分析中通常不考虑压痕的“桩-积”效应,即材料在压头周围发生隆起。这种现象会导致接触面积被低估,从而影响测量结果。桩-积通常发生在完全加工硬化的材料中,对于薄涂层下的软韧材料,由于塑性变形区受到约束,这种效应更为明显。据报道,桩-积材料对硬度测定的影响(有效增加了接触面积)比对压入模量的影响更显著。使用原子力显微镜(AFM)评估压痕形貌是判断是否存在桩-积的有效手段。
仪器必须按照 ISO 14577-2 的程序进行校准。在使用新压头前,必须完成仪器柔度 Cf 和压头面积函数 Ap(hc) 的校准/验证。在开始压痕循环之前,仪器必须达到所需的机械和热稳定性。数据分析与结果评估
通常将测得的复合性能(EIT, HIT)表示为接触半径 a 或压入深度 hc 与涂层厚度 tc 归一化后的函数。接触半径 a 可通过投影面积 Ap 近似计算: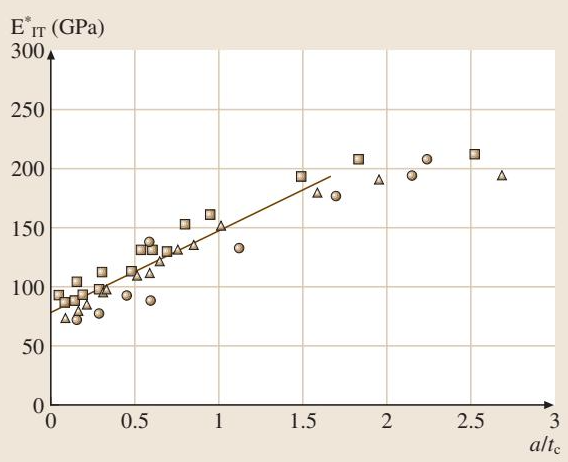
图4 压入折合弹性模量与归一化接触半径的关系图(示例:Au on Ni),展示了球形(●)、伯克维奇(▲)和维氏(■)压头的测试数据
测试过程中,热漂移是不可忽视的误差来源。图5提供了一个估算热漂移的决策树。如果漂移率显著,应在接近零力或90%卸载力处进行保载,测量并校正位移数据。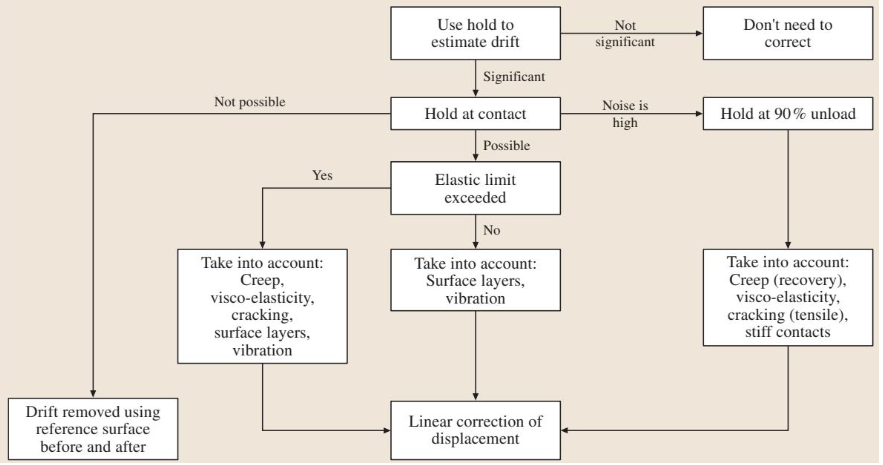
图5 辅助估算力控实验中漂移的决策树仪器柔度与压头面积函数的确定流程
总测量柔度 CT 是接触柔度 Cs 和仪器机架柔度 Cf 的总和:
其中,CT 来自未校正的卸载曲线在最大力处的导数,而 Cs 是与材料性能和接触面积相关的量。联立相关公式后可得:
这个公式揭示了一个关键方法:如果假设弹性模量恒定,那么对于给定材料,绘制 CT 相对于 A-1/2 的曲线应为线性。这条直线在纵轴上的截距,直接给出了仪器机架柔度 Cf。
这是一个迭代优化的过程:


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价