可靠性试验策略：应对不完整数据的实用方法

在理想的可靠性分析模型中，我们通常假定已掌握了完整的失效数据，即所有测试样本在观测周期内均已失效。然而，工程实践的复杂性远超于此。无论是实验室的可靠性测试，还是基于市场保修数据的分析，我们几乎总会面临样本量有限、测试时间受限或数据记录不完整的挑战。本文将深入探讨在这些约束条件下，如何设计试验策略并生成有价值的可靠性数据。

删失试验 (Censored Tests)

所谓删失试验，是指试验中止时，并非所有样本都发生了失效，或者并非所有失效都被纳入最终分析。这种情况在实际工作中非常普遍，其原因主要包括：

• 非预期失效模式：部分样本出现了与研究目标无关的失效模式，需要将其从数据集中剔除。
• 时间与成本约束：需要在试验完全结束前，对现有数据进行中期分析，以尽快获得结论。
• 现场数据分析：分析市场返修数据时，除了已失效的产品，大量仍在正常服役的产品也必须被纳入考量，这些未失效品即被视为“悬置项” (suspended items)。

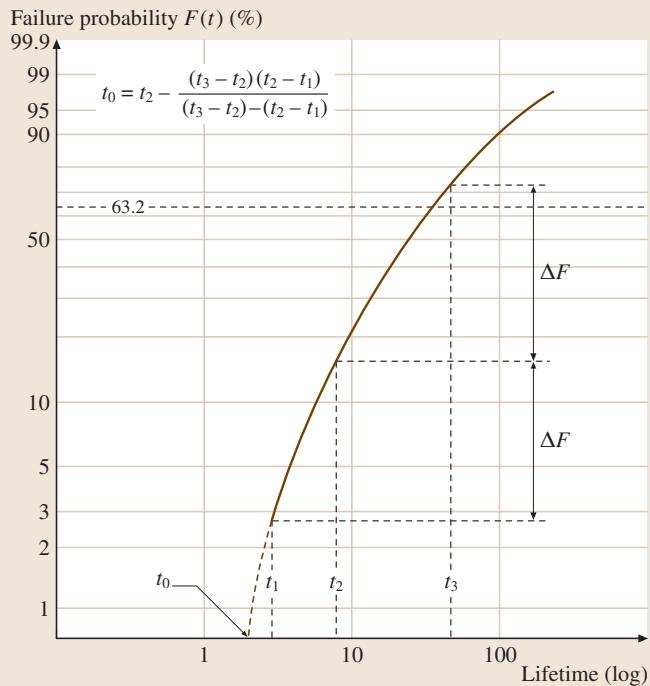
图1：利用Dubey方法估算无失效时间 t₀

删失数据的类型多样，这里我们聚焦于几种最核心的情形，如下图所示：

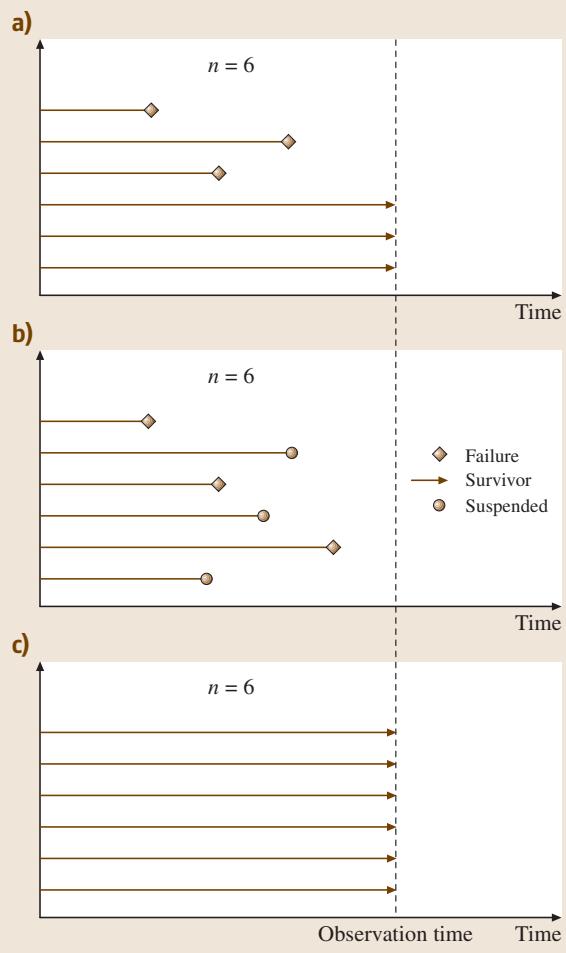
图2：可靠性试验期间的不同事件：(a) 部分样本失效(●)，部分存活(→)；(b) 部分样本失效(♦)，部分因其他原因被中止试验(●)；© 所有样本均通过试验。

接下来，我们将探讨如何分析这些情况下的数据。

情形 (a)：部分样本失效，部分存活

这种情况在处理现场数据时尤为常见。例如，一批设备交付客户使用一段时间后，部分发生故障，其余仍在正常运行。对此类数据的威布尔分析，其处理方式与完整数据基本一致，但必须注意，计算时所用的总样本数 n 应包含所有样本，即失效品与存活品的总和。在图2的示例中，n 应为6，而非3。

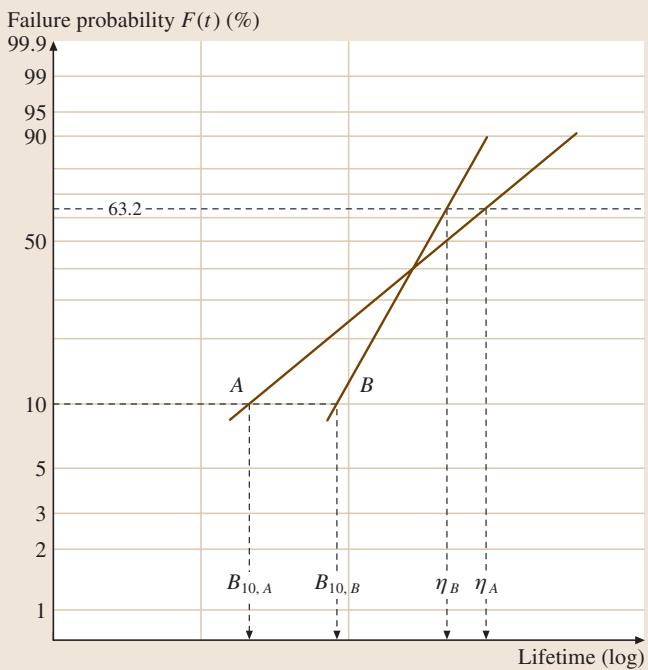
图3：对两种不同材料A和B进行威布尔分析，以决策何者更优。从特征寿命看，η_A > η_B，似乎材料A更好。但比较B₁₀寿命，结论恰好相反。在实际应用中，低失效概率区间的性能至关重要，因此B₁₀寿命通常是更有力的评判依据。本例中，材料B应被视为优于材料A。

情形 (b)：部分样本失效，部分被中止试验

当数据中包含因非目标失效模式而被中止的样本（悬置项）时，威布尔分析需要采用一种略有不同的技术。核心在于，我们不能再简单地为所有样本赋予 i = 1...n 的秩次，因为悬置项的存在给其后失效样本的真实排序带来了不确定性。我们需要计算一个调整后的平均秩次。

具体步骤如下：

1. 数据整理：收集所有数据，标记每个数据点的事件类型为“失效 (F)”或“悬置 (S)”，并按寿命从小到大排序，如表1所示。
2. 计算调整秩次：仅为失效样本计算新的秩次位置。悬置数据本身不参与秩次计算，但会影响后续失效样本的秩次。第 j 个失效样本的秩次 i_j 由前一个失效样本的秩次 i_{j-1} 和一个增量 y_j 决定： i_j = i_{j-1} + y_j 其中，增量 y_j 的计算公式为： y_j = (n + 1 - i_{j-1}) / (1 + n - j) 这里 n 是总样本数（包括失效和悬置），n-j 是排在当前第 j 个条目之后的剩余条目数。
3. 计算中位秩：根据新的秩次 i 计算失效概率（中位秩）。
4. 执行威布尔分析：使用计算出的失效概率和对应的寿命数据进行标准的威布尔绘图与分析。

表1：存在删失数据时调整秩次的计算示例 (n=6)

这种秩次调整的计算过程相对复杂，需要精确处理每个数据点，以确保最终分析的有效性。这正是专业检测实验室的核心价值所在，通过严谨的数据处理流程，确保从不完整数据中提取出最可靠的结论。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测寿命数据分析，可靠准确。欢迎沟通交流，电话19939716636

情形 ©：所有样本均在役 - 成功运行试验 (Success Run)

成功运行试验是可靠性工程中的一个强大工具，它巧妙地将测试样本数量和测试时间结合起来，并直观地体现了置信区间的意义。

典型任务场景是：我们需要在给定的要求寿命 L_dem 下，保证产品的最低可靠度 R_i,min。为此，我们使用有限数量的样本（例如 n=3）进行时长为 t_test 的试验。

假设产品寿命服从威布尔分布，该试验的评估公式为： R_i,min(L_dem) = (1 - α)^[1 / (n * (t_test / L_dem)^β)]

该公式的含义是：如果有 n 个样本在时长为 t_test (通常 t_test > L_dem) 的试验中全部存活，我们就可以在置信度为 α 的水平上，保证产品在要求寿命 L_dem 时的最低可靠度为 R_i,min。

在实际操作中，通常是先给定置信度 α 和最低可靠度目标，然后通过该公式反算出需要投入的样本数量 n 和必须达到的测试时间 t_test。图4清晰地展示了保证的最低可靠度与寿命比 (t_test / L_dem) 及样本数之间的关系。

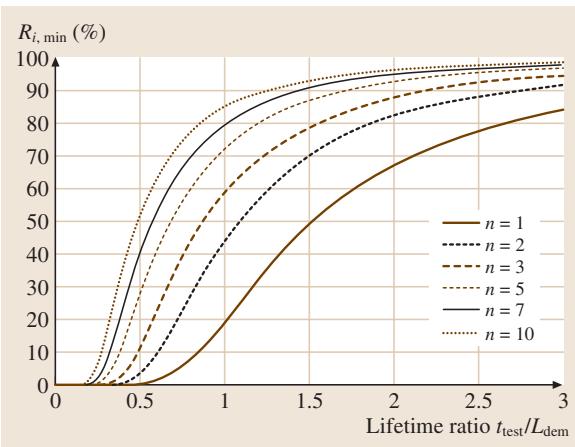
图4：成功运行试验中，保证的最低可靠度 R_i,min 作为寿命比和样本数 n 的函数。该图表明，样本数越少，要达到相同的可靠度水平，试验时间就必须越长。一个实用的经验法则是：当3个样本能够存活于2到2.5倍要求寿命的测试时，通常可以保证90%的可靠度。

该方法的主要局限在于，威布尔形状参数 β 必须是已知的，无法通过此方法确定。它需要依赖历史经验、类似研究或在简化条件下的预备试验来获取。

突死试验 (Sudden Death Test)

对于大批量样本，若要进行耗时极长的寿命试验，突死试验是一种广受欢迎的替代方案。其前提是试验设备能支持所有样本同时进行测试。因此，当试验台架资源充足但测试时间紧张时，该方法尤为适用。

其基本思路如下：

1. 取样：获取一个较大的总样本 (例如 n > 20)。
2. 分组：将总样本随机分为 m 个子样本组，每组 k 个样本（例如，n=20, m=4, k=5）。
3. 并行测试：同时对所有子样本组中的所有样本进行寿命试验。
4. 截尾：在任一子样本组中，一旦出现第一个失效样本，该组的试验立即停止。记录下这个首个失效样本的寿命。
5. 重复：对所有 m 个子样本组重复步骤3和4，最终得到 m 个首失效寿命数据。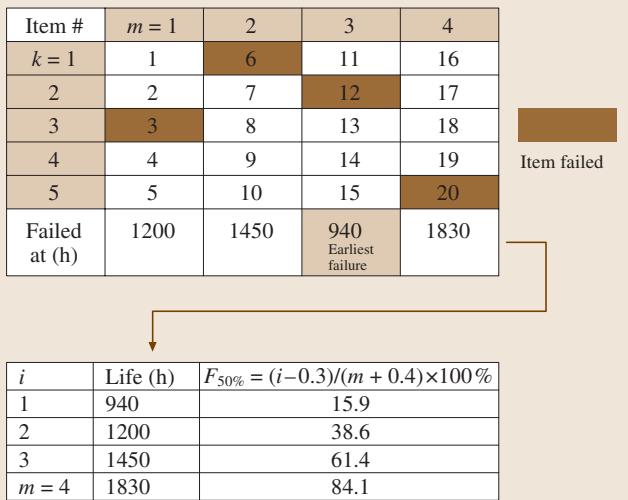

图5：突死试验的示意图。样本被分为m个大小为k的小组。每组的首次失效会中止该组所有样本的试验。将这些首失效数据按升序排列并计算失效概率。

6. 分析首失效数据：对这 m 个首失效寿命数据进行标准的威布尔分析。计算中位秩时，用子样本组数 m 替代总样本数 n： F(t_i) = (i - 0.3) / (m + 0.4)，其中 i = 1...m
7. 绘制首失效威布尔线：将数据点绘制到威布尔概率纸上，得到首失效样本的威布尔分布线。
8. 推断总体分布：通过特定的图解法或计算，从首失效的威布-尔线推导出原始总体（n个样本）的威布尔分布线。

尽管现代可靠性软件能够直接从失效数据便捷地计算出威布尔参数，但理解上述步骤的底层逻辑对于正确设计试验和解读结果至关重要。

退化试验 (Degradation Tests)

退化试验是一种较新的方法，近年来吸引了大量研究。该方法适用于那些存在某个可在运行期间被测量、且其变化能表征产品退化过程的参数。将该参数随时间（或使用量）的变化绘制出来，就构成了所谓的“退化路径”。

一个直观的例子是，通过在测试中定期测量汽车轮胎的磨损深度，并将其与行驶里程绘制成图。我们可以利用这些数据点外推出更长里程后的磨损情况，从而预估轮胎达到临界磨损值（即失效）时的时间。对 n 个被测设备进行同样的操作，就可以得到 n 个外推的寿命数据，这些数据可以用于标准的威布尔分析。

这种方法的最大优势在于，试验可以在远小于预期寿命的时间点被截断，从而大幅缩短研发周期。目前，关于设备需要测试多长时间才能保证外推结果足够准确的研究仍在进行中。

案例分析：某铁电存储芯片通过极化状态来区分逻辑“1”和“0”。其失效判据是：经过 N 次极化反转（循环）后，极化强度 P(N) 不得低于初始值 P_0 的80%。现对4个样本进行循环测试，并在特定的循环次数后测量 P(N)。为节省时间，试验在 10⁸ 次循环后截断，此时所有样本均未达到失效判据。根据文献可知，P(N) 与 N 存在 P(N) / P_0 = exp(-N / N*) + C 的关系（N* 和 C 为常数）。我们可以用此模型拟合已有的数据点，并外推至超过 10⁸ 的循环次数，从而找到每个样本达到失效判据（P(N) / P_0 = 80%）时的寿命 L_i。有了这组寿命数据 L_i，便可进行前述的威布尔分析。