从信号响应数据构建检出概率(POD)函数

在无损检测（NDT）领域，评估一种检测方法的有效性，核心在于量化其发现特定尺寸缺陷的能力。检出概率（Probability of Detection, POD）曲线，即 POD(a) 函数，正是实现这一目标的关键工具。它描述了检测系统成功发现尺寸为 a 的缺陷的概率。本文将深入探讨如何从最基础的检测信号响应数据出发，构建起严谨的 POD(a) 数学模型。

信号响应与检出决策

无损检测的本质，是通过某种物理激励（如超声波、涡流、X射线等）与材料相互作用，并捕捉其响应信号来判断缺陷的存在。我们可以将这个响应信号的强度或某个关键特征，量化为一个与缺陷尺寸相关的参数，记为 â。

在实际操作中，检测系统并非对所有信号都做出反应。工程师会设定一个判别阈值 â_dec。只有当检测到的信号 â 超过这个阈值时，系统才会判定“发现了一个缺陷指示”。这个简单的决策规则，构成了POD分析的基石。

对于一个实际尺寸为 a 的裂纹，其产生的信号响应 â 并非一个固定值，而是受到多种因素（如探头位置、材料表面状况、仪器噪声）影响，呈现出一定的随机性。因此，我们可以用一个概率密度函数 gₐ(â) 来描述其分布。

基于此，尺寸为 a 的裂纹被检出的概率 POD(a)，就等于其信号响应 â 大于检出阈值 â_dec 的概率。用数学语言表达，即为对概率密度函数在阈值之上的部分进行积分：

$$ POD(a) = /int_{/hat{a}{/mathrm{dec}}}^{/infty}g{a}(/hat{a})/mathrm{d}/hat{a} $$

这个积分的物理意义非常直观：它计算了所有可能产生的、且强度足以触发检出判定的信号所占的概率总和。如下图所示，POD(a) 就对应了概率密度函数曲线下方，位于检出阈值 â_dec 右侧的阴影区域面积。

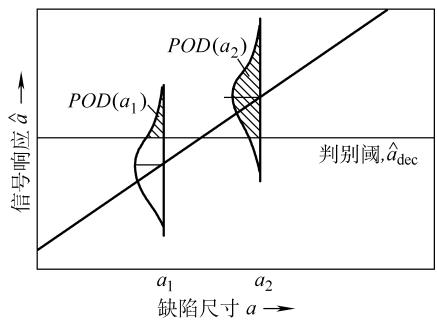图1 从 â 与 a 关系计算 POD(a) 的示意图

â-a 模型：关联信号与真实缺陷

为了让 POD(a) 模型具有预测能力，必须建立测量信号 â 与真实缺陷尺寸 a 之间的关联，这通常被称为“â-a 模型”。一个基础的线性关系可以表示为：

$$ /hat{a} = /mu(a) + /delta $$

此式中：

• μ(a) 代表缺陷尺寸为 a 时，信号响应 â 的平均值或期望值。它描述了信号强度随缺陷尺寸增大的宏观趋势。
• δ 是一个随机误差项，代表了所有不确定性因素的总和，使得 â 在其均值 μ(a) 周围波动。

大量的工程实践与数据分析表明，直接使用 â 和 a 的线性关系，在很多情况下并非最优。信号响应和缺陷尺寸往往跨越多个数量级，其间的关系在对数坐标下表现出更好的线性特征。因此，一个更常用且更稳健的模型是建立在 ln(â) 与 ln(a) 之间：

$$ /ln(/hat{a}) = /beta_{0} + /beta_{1}/ln(a) + /delta $$

这里的模型假设：

• β₀ 和 β₁ 是线性回归的常数系数，分别代表截距和斜率。
• 误差项 δ 服从均值为0，标准差为 σ_δ 的正态分布。

这种对数线性模型能够更好地处理数据的异方差性，是现代POD分析的标准方法。

推导 POD(a) 的闭合解形式

在上述对数线性模型的基础上，我们可以推导出 POD(a) 函数的一个解析表达式。检出的条件是 â > â_dec，在对数域中即为 ln(â) > ln(â_dec)。

因此，POD(a) 可以表示为：

$$ POD(a) = P[/ln(/hat{a}) > /ln(/hat{a}{/mathrm{dec}})] = P[/beta_0 + /beta_1/ln a + /delta > /ln(/hat{a}{/mathrm{dec}})] $$

整理后得到：

$$ POD(a) = P[/delta > /ln(/hat{a}_{/mathrm{dec}}) - (/beta_0 + /beta_1/ln a)] $$

由于 δ 服从正态分布 N(0, σ_δ²)，我们可以利用标准正态累积分布函数 Φ 来计算这个概率。Φ(z) 表示标准正态变量小于 z 的概率。利用正态分布的对称性 P(X > x) = 1 - P(X ≤ x)，可得：

$$ POD(a) = 1 - /phi /left[/frac{/ln(/hat{a}{/mathrm{dec}}) - (/beta_0 + /beta_1/ln a)}{/sigma{/delta}}/right] $$

再次利用标准正态分布的对称性 1 - Φ(z) = Φ(-z)，上式可以进一步化简，得到一个更直观的形式：

$$ POD(a) = /phi /left[/frac{(/beta_0 + /beta_1/ln a) - /ln(/hat{a}{/mathrm{dec}})}{/sigma{/delta}}/right] = /phi /left/{/frac{/ln a - [/ln(/hat{a}{/mathrm{dec}}) - /beta_0] / /beta_1}{/sigma{/delta} / /beta_1}/right/} $$

这个最终形式清晰地表明，POD(a) 是一个累积对数正态分布函数。这意味着，在对数尺度下，缺陷尺寸 ln(a) 服从一个正态分布。该分布的两个核心参数——均值 μ 和标准差 σ——可以由模型参数直接给出：

$$ /mu = /frac{/ln(/hat{a}{/mathrm{dec}}) - /beta_0}{/beta_1} $$ $$ /sigma = /frac{/sigma{/delta}}{/beta_1} $$

在实际应用中，要构建一个可靠的POD曲线，就需要通过大量的实验（即对一系列已知尺寸的缺陷进行检测）来获取成对的 (a, â) 数据。然后，可以采用最大似然法（Maximum Likelihood Estimation, MLE）等统计技术，对这些数据进行拟合，从而得到模型参数 β₀、β₁ 和 σ_δ 的最佳估计值。这个过程需要严谨的实验设计和专业的数据分析能力，以确保最终得到的POD曲线能够真实反映检测系统的性能。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测无损探伤检测，可靠准确。欢迎沟通交流，电话19939716636