要深入理解金属磁记忆检测方法的内在机理,我们必须从其物理根基——磁机械效应(Magnetomechanical Effect)谈起。尽管学术界对金属磁记忆的具体机制仍有探讨空间,但磁机械效应作为其核心原理已是共识。简单来说,该效应描述了铁磁性材料在受到应力作用时,其磁化强度发生变化的现象。这一力磁耦合现象不仅是理论研究的前沿,更在磁性传感器开发、无损检测中的应力测量等领域展现出巨大的工程应用价值。
磁机械效应的探索史几乎贯穿了整个现代物理学。其早期应用甚至带有战争的硝烟味:1939年,德军在泰晤士河口布下“磁性水雷”,利用舰船自身的磁场引爆水雷。同年,当苏联舰船也遭遇此类攻击后,其科学院院士Alexandrov首次从理论上解释了这一现象——舰船金属船体在地球磁场中,因振动载荷(一种应力形式)的影响,导致其磁化强度显著增大。
到了20世纪四五十年代,Bozorth、Liboutry等学者开始系统研究恒定外磁场下,应力加载如何改变材料的磁化强度,但当时的结论并不统一。
最初的理论探索建立在一个理想化的假设之上:磁机械效应是完全可逆的。其核心逻辑颇为直观:既然磁化能改变铁磁材料的尺寸(磁致伸缩效应),那么反过来,材料的应变(由应力引起)也理应能改变其磁化强度。Bozorth对此进行了深入探讨,而Cullity则依据热力学中的Le Chatelier原则,给出了一个经典的数学表达:
(dλ/dH)<sub>σ</sub> = (dB/dσ)<sub>H</sub>
这个公式优雅地将两个看似独立的物理过程联系起来。左边描述了在应力恒定时,磁致伸缩系数随外场的变化率;右边则是在外场恒定时,磁感应强度随应力的变化率。由于 B = μ(H + M) 且外场强度H不随应力变化,公式右侧实质上等于 μ<sub>0</sub>(dM/dσ)<sub>σ</sub>。此式成为了后续研究的理论基石,它准确地描述了微小应力下的可逆变化,并指出磁致伸缩应变率越大的材料,其磁机械效应也越显著。
然而,现实世界远比理想模型复杂。磁化过程天然伴随着磁滞损耗,不可逆的磁畴行为才是其本质特征,可逆变化仅仅是其中的一部分。
1949年,Brown提出了一个影响深远的理论,他尝试将不可逆性纳入考量。布朗理论假设,在微弱外磁场下,磁化强度的变化源于遵循瑞利(Rayleigh)原理的磁畴运动。瑞利原理主要用于描述低磁场下的磁滞行为,其关系式为:
B = μ<sub>0</sub>H ± ηH
Brown进一步假设,应力和外磁场对磁畴的作用可以等效为对磁畴壁的静压力,并据此推导出了理论曲线。
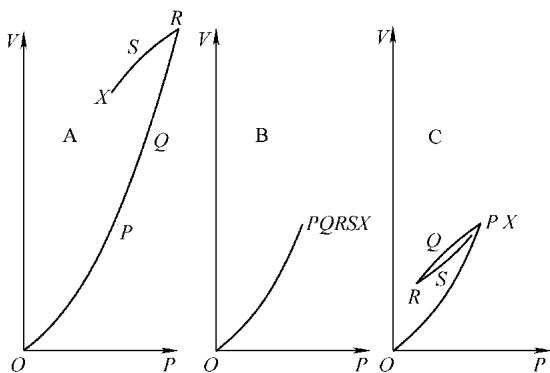
图1 各类畴壁的行为
然而,布朗理论很快就遇到了几个难以逾越的障碍。首先,应力是张量,而磁场是矢量,两者具有不同的对称性,将其简单等效在物理上是不严谨的。
其最致命的缺陷在于,该理论推断材料磁化强度在拉应力和压应力下的变化是相同的。这一推论源于对磁畴结构的分析:通常认为,应力只影响非180°畴壁(在钢铁中即为90°畴壁)。如果假设与外场方向一致和相反的90°畴壁数量均等,那么改变应力方向(从拉到压)仅仅是互换了这两种畴壁的作用,最终的磁化强度变化理应没有区别。
但实验结果无情地否定了这一推论。Craik和Wood的实验(如图2所示)清晰地展示了多种铁磁材料中普遍存在的“拉压应力不对称效应”。
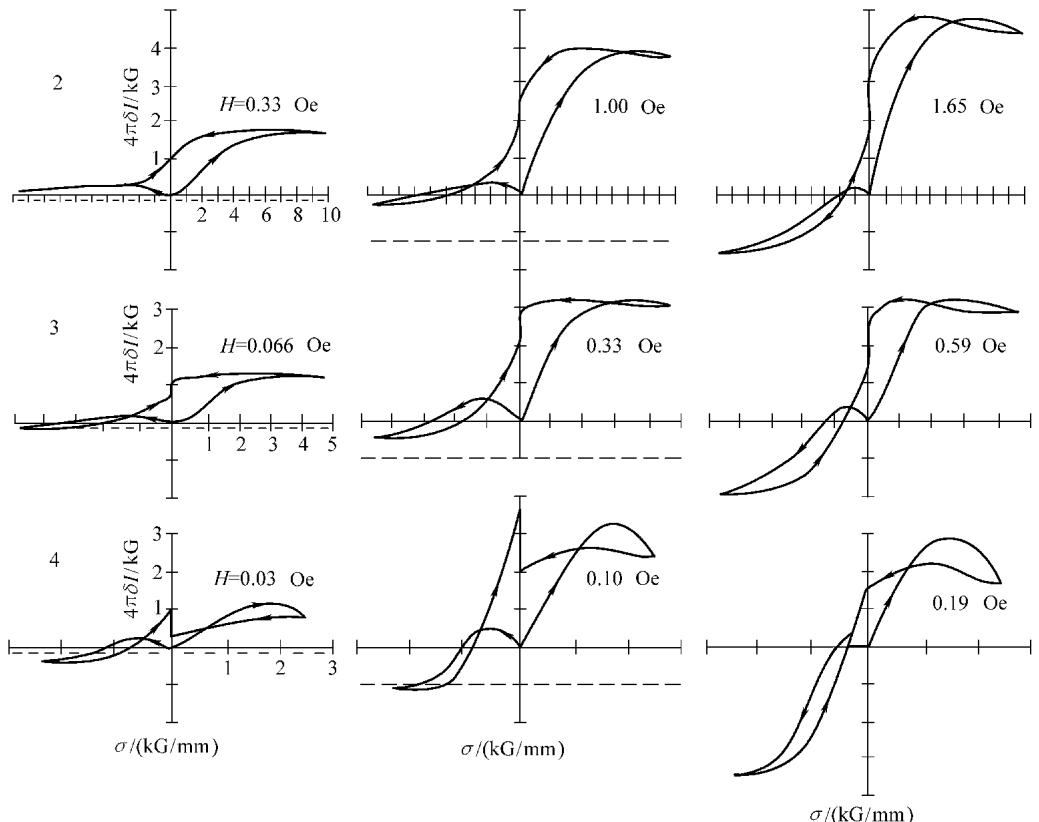
图2 软铁、普通硅铁等材料的应力磁化曲线试验结果
此外,该理论还预言,当应力从最大值卸载后,磁化强度将保持恒定。这同样与实验观测相悖。Craik和Wood因此断言,任何成功的磁机械效应理论都必须考虑应力作用下磁畴结构发生的不连续变化。Birss的后续研究进一步深化了这一认识,他指出应力对90°畴壁的作用远不止是驱动其运动,还包括改变畴壁节点的能量和造成磁畴结构的不可逆变化——而布朗理论只触及了第一点。这些复杂的实验现象和理论与实践的脱节,恰恰说明了精确表征材料力磁性能的难度。要获得可靠的实验数据,对测试环境、加载控制和信号采集都有着极高的要求。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测金属材料应力磁性分析,可靠准确。欢迎沟通交流,电话19939716636
20世纪80年代,研究迎来了新的曙光。Bozorth和Williams发现,对坡莫合金施加39MPa的应力后,其磁化曲线竟十分接近该材料的“非磁滞磁化曲线”——这是一个理想的、无能量损耗的磁化状态。
1984年,Jiles和Atherton等人基于这类观察,提出了一个全新的概念——“接近原理”(Principle of Approach)。他们定性地推测,循环施加的应力对材料磁化强度的影响,是一个驱动其剩余磁化强度不断向非磁滞磁化强度靠近的不可逆过程。磁感应强度的变化量,可能与当前磁状态和非磁滞状态之间的“距离”成正比。
Pitman的精巧实验为“接近原理”提供了有力证据。他研究了在同一外场下(80 A/m),处于不同初始剩余磁化状态的样品,其磁感应强度随应力的变化率 (dB/dσ)<sub>H</sub>。
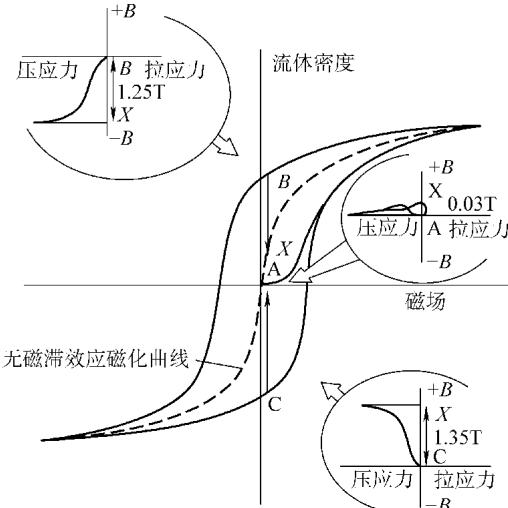
图3 剩余磁化强度的选取位置
实验发现(如图4),从正、负剩余磁化强度出发的样品,其磁化强度的变化几乎呈镜像对称。而初始状态接近退磁(即接近非磁滞状态)的样品,其磁化强度变化量则小得多。这揭示了一个关键规律:在相同的外力和外场下,磁化强度变化的方向,取决于其初始状态是在非磁滞磁化曲线的上方还是下方。
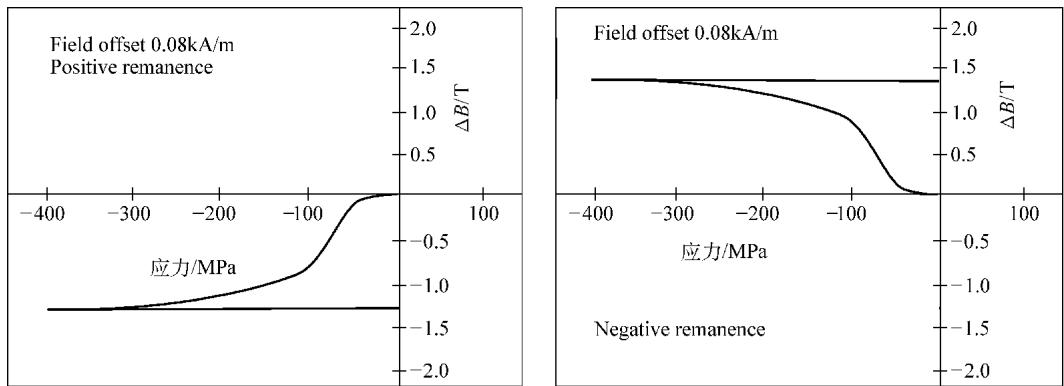
图4 正负剩余磁化强度试样的镜像对称结果
Maylin和Squire的研究进一步证实了这一点,但他们也补充道,这种向非磁滞状态的“趋近”主要适用于对称磁滞回线上的点。对于非对称回线上的点,应力会使其趋向于某个不等于非磁滞磁化强度的平衡值。他们总结出决定磁机械效应变化方向和大小的三个核心因素:
1995年,Jiles提出了一个更为完善的磁机械效应理论。他回归到将应力作用等效为外加磁场的思路,但这一次,分析的起点是能量。
Jiles从系统能量增加的角度出发,构建了如下模型:
A = μ<sub>0</sub>HM + (μ<sub>0</sub>/2)αM<sup>2</sup> + (ν/2)σλ + TS
这个模型的精妙之处在于,它将应力(σ)作为系统能量的一部分。通过对总能量A关于磁化强度M求导,可以得到一个“等效场”(Effective Field):
H<sub>eff</sub> = (1/μ<sub>0</sub>)(dA/dM) = H + αM + (3/2)(σ/μ<sub>0</sub>)(dλ/dM)
在这个等效场中,由应力加载引起的部分被明确地分离出来:
H<sub>σ</sub> = (3/2)(σ/μ<sub>0</sub>)(dλ/dM)<sub>σ</sub>
Jiles的理论通过能量的视角,最终将应力的作用量化为了一个等效的磁场 H<sub>σ</sub>,为力磁耦合现象提供了坚实而自洽的物理图像。
回顾磁机械效应的研究历程,我们看到理论模型从简单的可逆假设,到考虑磁畴运动的布朗理论,再到基于大量实验观测的“接近原理”,最终发展到以能量为核心的Jiles理论。这一系列工作基本厘清了在微弱磁场环境下,均匀应力如何引起材料磁场的变化。
当然,真实工况下的金属磁记忆现象要复杂得多,它涉及非线性的应力分布(如应力集中区),外部磁场也远不止微弱的地磁场。尽管如此,上述这些关于均匀应力下磁机械效应的基础研究,是构建更复杂力磁耦合模型的基石,为我们今天利用磁信号进行结构健康监测和失效分析奠定了不可或缺的理论基础。


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价